초록배경 및 목적이번 연구는 국어와 수학의 학업 관계 발달 연구를 통해 언어발달장애 아동을 위한 학습지원 방안 마련의 기초를 마련하기 위함이다. 이를 위해 초등학교 입학 전 유치원 시기에서부터 초등학교 입학 후 4학년까지 동일한 대상자들의 연령 증가에 따른 국어와 수학 학업수행 능력의 발달정도와 발달관계를 살펴보았다.
방법한국아동패널연구(PSKC, Panel Study on Korean Children) 연구 대상자 중 2014년(7차년도, 6세)부터 2018년(11차년도, 초등학교 4학년)까지의 국어와 수학 학업수행 능력 평가 결과에 대해 잠재성장모델링 분석(Latent Growth Curve Analysis, LGCA)을 실시하였다.
AbstractObjectivesThis study is a foundation for preparing learning support measures for children with developmental language disabilities through research on the academic relationship development of the Korean language and mathematics. The degree and developmental relationship of Korean language and mathematics academic performance according to age from kindergarten before entering elementary school to 4th grade were examined.
MethodsLatent Growth Model Analysis (LGMA) was conducted on the results of the evaluation of Korean language and mathematics academic performance from 2014 to 2018 (4th grade in elementary school).
ResultsKorean language and mathematics developed with significant influence on each other. It was confirmed that the basic ability to perform the Korean language has a significant effect on both the basic ability and the change in the academic ability in mathematics. It is a fact that Korean language ability is the basis of mathematical academic ability through the implementation of the mathematical sentence system. In addition, although Korean language ability and mathematics influence each other, in the case of mathematics, the cognitive ability of individual children played a more significant role compared to the Korean language in the academic performance results.
유치원 과정에 속하는 만 3-5세 일반 아동들은 언어 발달에 있어 문장표현이 급격하게 성장하는 시기이다. 그리고 이 시기에 아동들은 수 인지 능력도 발달하는데 이때 수 인지에서 언어의 효과를 구분하여 평가하는 것은 매우 어렵다. 왜냐하면 수와 언어는 통합적으로 발달하고 있기 때문이다. 이 시기의 아동들은 수 세기를 말로 표현할 수 있으며, 이러한 수 개념 발달은 일반적인 발달에 속한다. 그리고 아동기에 수와 관련된 어휘 이해와 수 세기 능력은 이후 수학 학습의 중요 요인으로 알려져 있다(Steffe, 1992).
언어장애가 있는 아동 중 수학관련 어휘에 대한 이해가 어렵고, 이 때문에 수 인지 발달에 문제를 보이는 대상자들이 존재한다(Arvedson, 2002; Fazio, 1996). 그리고 언어 구문 능력에 어려움을 보이지만 수 인지능력에 있어서는 정상발달을 보이는 대상자들도 있다(Bideaud, Meljac, & Fischer, 1992; Gelman, 1997; Gersten & Chard, 1999). 이렇듯 자연적 언어와 수 인지는 어떠한 면에서는 매우 밀접한 발달을 보이는 것으로 여겨지지만, 한편으로는 매우 구분되는 능력인 것으로 여겨진다.
언어와 수 인지와의 발달 관련성의 정도에 따라 언어발달지체 아동의 학습지원이 달라질 수 있다. 이에 이번 연구는 국어와 수학의 학업 관계 발달 연구를 통해 언어발달장애 아동을 위한 학습지원 방안 마련의 기초를 마련하고, 통합교육에서의 언어치료와 학교 교육과정 구성의 연구지원을 위한 기초연구를 진행하였다.
대한민국 교육부는 2019년 7월 24일에 2020년 유치원 누리과정을 새로 고지하였으며, 2021년 11월 24일에는 초 · 중 · 고등학교 교육과정 전체에 대한 ‘2022년 개정 교육과정’을 발표하였다. 만 3-5세 아동을 대상으로 진행되는 누리과정은 어린이집과 유치원에서 만 3-5세까지의 유아를 대상으로 적용되는 교육과정이다. 0-2세 어린이집 보육과정과 초등학교 교육과정과의 연계성을 고려하여, 누리 과정은 신체운동 · 건강, 의사소통, 사회관계, 예술경험, 자연탐구의 5개 영역을 중심으로 학습이 구성되어 있다(Ministry of Education, 2019).
누리과정의 의사소통 영역 학습은 듣기와 말하기를 중심으로 이루어지며, 읽기와 쓰기에 관심을 가질 수 있는 초기 문해 학습(주변 상징과 글자에 관심 갖기, 생각을 글자와 비슷한 형태로 표현하기, 책과 이야기 즐기기) 또한 중요하게 다루고 있다. 그리고 자연탐구 영역에는 생활 속에서 탐구하기(물체를 세어 수량을 알아보기, 물체의 위치와 방향, 모양을 알고 구별하기, 일상에서 길이, 무게 등의 속성을 비교, 주변에서 반복되는 규칙을 찾기, 일상에서 모은 자료를 기준에 따라 분류, 도구와 기계에 대해 관심을 갖기) 부분에 수리적 요소를 포함하고 있다(Ministry of Education, 2019). 즉, 유아들은 누리과정에서부터 국어와 수학 기초학습을 수행한다.
초 · 중 · 고등학교 학생들을 위한 ‘2022 개정 교육과정 총론’에서는 고교학점제를 위한 과목 선택권 확대, 지식과 과정 태도를 아우르는 핵심 교과역량 강화, 초등학교 선택과목 도입(생태교육, 민주 시민교육 인공지능으로 알아보는 우리 고장, 지역과 민주시민, 역사 체험 등), 그리고 여러 교과를 학습하는 데 기반이 되는 언어, 수리, 디지털 소양과 같은 기초소양을 강조하고 있다. 즉, 개정 교육과정은 학교와 학생들의 자율과 선택을 확대하고 학생의 기초학력과 디지털리터러시를 강화하는 방안으로 초점이 맞춰졌다(Ministry of Education, 2021). 미래 인재역량을 위한 이와 같은 2022 개정안을 자세히 살펴보면, 이전 개정안과는 달리 교과통합을 통한 생활중심의 학습과 기본적인 언어와 수리에 대한 역량이 강조되고 있다.
2022 개정 교육과정 학습연계에 있어, 국어와 수학은 계속해서 중요한 기초학력 과목으로 다루어지고 있다. 교육과정 개정을 통해 생활중심의 학습을 강조하면서, 초등학교에서의 국어는 듣기와 말하기를 기반으로 하여 읽기와 쓰기 문해력 향상을 강조하고 있으며, 수학은 문장제를 강화한 연산 도출 과정에 대한 이해를 중시하고 있다(Ministry of Education, 2021). 즉, 수학 학업 능력 향상을 위해서는 시각적 이미지와 수학적 상징을 언어로 표현할 수 있는 역량이 강조되고 있다. 그리고 수학 문장제는 구문 언어와 수학관련 낱말(더하기, 빼기, 나누기, 얼마나 더, ~보다 크다/작다, 앞/뒤/옆/위, 크기, 비교, 넓이, 깊이, 도형, 다각형 등)에 대한 기본적 이해 능력이 있어야 풀이가 가능하다(Toll & Van Luit, 2014). 그러므로 현재 및 미래 사회에서의 수학은 점점 언어와 매우 밀접한 관련이 있는 학문으로 발달하고 있다.
모든 학습의 기본은 언어이기 때문에, 학령전기와 학령기초기에는 언어 발달의 문제가 중요하게 다루어지고 있으며 이러한 방향성은 타당하게 받아들여지고 있다(O’Halloran, 2005; Toll & Van Luit, 2014). 하지만 수학은 언어 능력과 독립적인 학문으로 해석할 수 없다. 국어와 수학은 그 상징의 종류, 해석과 적용에 있어서는 차이를 보이지만 언어와 수학은 모두 상징을 통한 의사소통이라는 공통점이 있기 때문이다(Whitin & Whitin, 2000). 수학은 기호학적 개념으로 살펴보았을 때 언어와 시각적 이미지, 수학적 상징들로 구성되어 있다(O’Halloran, 2005). 그리고 기초 수학 능력 습득은 말 발달과 높은 상관을 보인다(Toll & Van Luit, 2014). 즉, 적합한 언어기술은 초기 수학 학습을 위한 선행 조건이 된다. 그리고 언어 능력은 수학 수행의 구성개념이기도 하면서 학령기 이후의 수학 수행 능력의 예측 요인과도 관련이 있는 것으로 나타났다(Toll & Van Luit, 2014). 또한 언어 능력이 또래보다 낮은 아동들은 초기 수학 학습에서도 또래보다 늦은 발달을 보이는 경향이 나타났다(Kleemans, Segers, & Verhoven, 2011).
근래 임상과 연구현장에서는 언어발달장애 아동의 비언어적 역량 또는 수리적 능력, 수학 학업 능력 등에 대한 관심이 집중되었다. 즉, 단순언어장애 아동의 수리 능력을 살펴본 연구들과 난독증 아동의 수학 능력 발달과 관련된 연구들이 진행되었다(Arvedson, 2002; Cowan, Donlan, Newton, & Lloyd, 2008; Dowker, 2008; Ellis, Miles, & Wheeler, 2008; Fazio, 1999; Koponen, Mononen, Räsänen, & Ahonen, 2006; Windsor, Kohnert, Loxtercamp, & Kan, 2008). 이러한 연구의 공통점은 언어 발달의 문제가 언어만의 문제가 아니라 다른 인지적 처리 능력의 문제와 관련되어 있다는 것이다. 특히 단순언어장애 대상자들은 언어 발달의 문제와 함께 수학 능력도 발달지체를 동반하는 것으로 나타났다(Arvedson, 2002; Cowan et al., 2008; Dowker, 2008). 또한 난독 아동의 경우는 초등학교 4학년까지는 수학 풀이 정확성이 또래 아동들에 비하여 유의미하게 낮으며 또한 처리 속도가 매우 느린 것으로 나타났다(Ellis et al., 2008). 이러한 연구결과를 통해 언어 발달의 문제가 수학 능력 발달에 제한적 요소가 될 수 있으며, 특히 언어발달장애 아동의 경우 수학역량 발달 문제를 동반하는 경향이 있음을 확인하였다(Arvedson, 2002; Cowan et al., 2008; Dowker, 2008).
초기 언어와 수학 능력은 서로 관련되어 발달하고 있다. 다른 인지적 요소(주의, 기억, 정서 등)들이 그러하듯이 유치원 및 어린이집 누리과정 시기에 언어와 수학은 상호 발달에 영향을 미친다 (Toll & Van Luit, 2014). 일반적으로는 언어가 학습의 주요 발달을 돕는 요인으로 알려져 있다. 그렇지만 언어와 수학 발달이 복잡한 관계 발달을 하고 있기 때문에 언어와 수학 발달의 관계성과 상호간 원인관계를 결정하는 것은 어려울 수 있다. 일반 아동의 경우는만 3세 이후 어휘를 조합하여 문장으로 산출하고 상황과 맥락에 적절하게 문장으로 표현하고, 또한 복문을 이해하는 능력이 급격히 발달하게 된다(Paul, Norbury, & Gosse, 2017). 그러므로 유치원과 어린이집 누리과정에서는 의사소통 능력을 강조한 학습이 이루어지고 있다. 하지만 수학이 언어와 유사한 처리과정이 이루어지는 상징언어의 일종이라면 수학적 기호 상징을 언어를 통해 이해하고 표현하는 과정은 의사소통 속에 포함되어 강조되어야 한다(Toll & Van Luit, 2014). 그리고 유치원 시기에 언어와 수리 역량에 문제가 있던 아동들은 이후 학령기에도 여전히 언어와 수학 학습에 지체를 동반할 가능성이 높다(Toll, Van der Ven, Kroesbergen, & Van Luit, 2011). 그러므로 학령 전 누리과정(만 3-5세 아동에게 주어지는 유치원과 어린이집 공통교육과정) 시기에 언어와 수학 능력에 발달 위험 요소가 있는지를 살펴보는 것은 이후의 초등학교 학령기 준비를 위한 학습계획에 있어 중요한 학습 능력 예측요인으로 작용한다(Mazzocco, 2005).
현재 국내에서는 국어와 수학 능력과의 관계를 살펴본 연구는 많지 않다. 하지만 몇몇 연구들을 통해 국어와 수학과의 관련성을 확인할 수 있었다. Park (2019)의 연구에서는 일반 초등학교에 재학 중인 초등학교 4-6학년 68명을 대상으로 음악 능력(음고 지각력, 박 지속력, 리듬 재현력)과 언어 능력(언어지능), 수학 능력(수학논리지능)의 상관관계 연구결과, 음악과 언어, 수학은 서로 유의미한 상관관계를 보이는 것으로 나타났다. 그리고 일반 초등학교 3학년 340명을 대상으로 수학 문제해결 능력과 국어(말하기, 듣기, 읽기, 쓰기) 능력 간의 상관관계를 살펴본 연구결과, 수학 문제해결 능력은 국어의 읽기 능력과 가장 높은 상관을 보이는 것을 확인하였다 (Song, 2010). 이들 연구들은 언어와 수학의 상관만을 본 연구들로 유의미한 관련성을 살펴보았을 뿐, 국어와 수학의 상호관계성과 발달관계에 대해서는 구체적으로 연구가 진행되지는 못하였다. 이에 이번 연구에서는 국어와 수학과의 발달관계를 살펴보았다.
한국아동패널은 2008년 4-7월생 아동패널이 20세가 되는 2027년까지 종단으로 인간 발달을 연구하고 있다. 패널 대상자들은 연령에 따라서 적합한 과제를 이용하여 부모 및 형제자매, 또래관계, 인지, 언어, 학습과 사회정서 등을 매년 종단으로 평가를 받고 있다. 다양한 평가과제 중 6세 누리과정에서는 학업 능력, 초등학교 1학년부터 6학년까지는 학업수행 능력이 포함되었으며 이러한 과제 모두 국어와 수학 능력을 포함하고 있다. 그러므로 이번 연구는 한국 아동패널 데이터를 이용하였다. 하지만 패널 대상자들이 초등학교 5학년이 된 2019년과 6학년인 2020년에는 학업 능력 데이터에 대한 결손이 많아서 이전 년도에 비하여 평가를 완료한 대상자가 50명 이하의 수준이었다. 이에 종단연구를 분석하는 데 있어 연구의 효과를 살펴보기 어려운 한계가 있었다. 이에 주요 연구 대상자 연령을 만 6세에서 초등학교 4학년까지로만 제한하여 데이터를 분석하였다. 즉, 이번 연구는 초등학교 입학 전 유치원 시기에서부터 초등학교 입학 후 4학년까지 동일한 대상자들의 연령 증가에 따른 국어와 수학 학업수행 능력의 발달정도와 발달관계를 살펴보았다. 구체적인 연구문제는 다음과 같다.
연구문제 1. 학업수행 능력(학령전 언어 및 문해 능력, 학령전 수리적 사고, 초등학교 국어, 수학 수행평가 결과) 변수들의 상관관계는 어떠한가?
연구문제 2. 예비 초등학생 시기부터(만 6세) 초등학교 4학년(10세)까지의 국어와 수학 학업수행 능력 잠재성장모델은 어떠한가?
연구문제 3. 초등학교 4학년 국어와 수학 학업수행 능력을 예측하는 관측 학업수행 능력 변수는 무엇인가?
연구방법연구대상한국육아정책연구소(KICCE, Korea Institute of Child Care and Education)는 아동의 성장 · 발달을 이해하고 이에 영향을 미치는 요인을 파악하기 위해서 2008년 4월에서 7월 사이에 의료기관에서 출생한 신생아 2,000가구를 조사 모집단 표본으로 하여 이들이 성인기에 접어드는 2027년까지 총 20년간 전반적인 아동 발달 특성과 부모 특성, 가정 환경 특성, 교육(학교 및 사교육) 특성, 지역사회 특성, 정책 특성 자료를 수집하는 장기 종단연구인 한국아동패널연구(PSKC, Panel Study on Korean Children)를 진행하고 있다.
이번 연구에서는 PSKC의 2014년(7차년도, 6세) 6월부터 12월까지 약 6개월간 진행된 학업 능력(언어 및 문해 능력, 수리적 사고) 패널연구에 참여하고, 이후 2015년(8차년도, 초등학교 1학년)부터 2018년(11차년도, 초등학교 4학년) 학업수행 능력(국어, 수학) 평가에 모두 참여한 대상자만으로 하였다. PSKC의 원 데이터는 2020년까지 현재 공개되어 있지만 2019년 대상자들의 데이터가 결측 처리된 대상자가 많아 종단연구결과 제시에 적합하지 않다는 판단 하에 2019년과 2020년 데이터는 제외하고 분석하였다. 즉, 6세 유치원 시기 학업 능력 평가부터 초등학교 입학 이후 1학년에서 4학년까지 학업수행 능력 평가 모두에 참여한 133명만을 대상으로 분석하였다(Table 1).
대상자 133명 중 종단과제 모두에 참여한 아동의 성별 비율을 살펴보면 남학생은 69명(51.88%)였으며 여학생은 64명(48.11%)로 성별에 따른 참여자의 차이는 유의미하지 않았다(χ2 (1, 133) =.19, p=.67). 그리고 참여 대상들 모두는 2008년에 태어난 대상자들로 연령은 모두 동일하였으며 이중 2008년 4월에 태어난 아동은 35명(26.32%), 5월에 태어난 아동은 53명(39.85%), 6월에 태어난 아동은 34명(25.56%), 그리고 7월에 태어난 아동은 11명(8.27%)이었다. 대상 아동은 대부분 4-6월에 태어난 아동이 대부분을 차지하였다(χ2 (3, 133) = 26.73, p<.001).
측정 도구학업 능력(Academic skills)6세 아동을 대상으로 진행한 한국아동패널의 학업 능력(Academic Skills) 평가 문항은 ‘언어 및 문해 능력(Language and Literacy)’과 ‘수리적 사고(mathematical thinking)’ 문항으로 구성되었다. 한국아동패널 학업 능력 평가 문항은 미국 ‘국립아동보건인적개발원(National Institute of Child Health and Human Development, NICHD)’의 2단계 연구인 ‘아동 및 청소년 발달 연구(Study of Early Child Care and Youth Development, SECCYD)’에 적용된 학업 능력 과제를 번안 수정한 것이다.
NICHD SECCYD는 54개월에서 초등학교 1학년 시기의 아동을 대상으로 학업 능력 검사(언어 및 문해 능력 15문항, 수리적 사고 10문항)를 진행하였다. 한국아동패널 연구진은 NICHD SECCYD의 학업 능력 검사 문항을 한국어로 번역하여, 국내 아동을 대상으로 예비조사를 실시하였다. 그 결과 언어 및 문해 능력은 영어 표현 15개 문항 중 13개 문항을 선정한 후에 한국어 특성을 반영한 쓰기 관련 1문항을 추가하여 총 14개 문항을 구성하였다. 그리고 수리적 사고 능력은 영어 표현 10문항에 한국적 표현에 적합한 수리적 사고 5문항을 추가하여 15개 문항으로 구성하였다(Table 2, Appendix 1).
학업 능력 검사 문항은 종단연구 대상자들이 소속되어 있는 육아지원기관의 담임교사가 web 설문지를 통해 응답하도록 하였다. 이번 연구는 ‘언어 및 발현 문해 능력’ 14개 문항과 ‘수리적 사고’ 15개 문항, 총 학업 능력 29개 문항을 평가하여 분석하였다. 문항에 대한 점수화는 ‘아직 하지 않음(1점), 하기 시작함(2점), 어느정도 해냄(3점), 잘하는 편임(4점), 능숙함(5점)’과 같은 5점 리커트 척도 [5-point Likert-type scale; Not yet (1) - Beginning (2) - In Progress (3) - Intermediate (4) - Proficient (5)]를 사용하였다(Table 2). 이러한 범주화 점수에 대한 종단평가를 위해 이번 연구에서는 5점 척도 개별 문항의 합계 점수를 구하고 이를 다시 100점 만점으로 환산하여 사용하였다.
학업수행 능력(Academic performance)한국아동패널 연구에서 초등학생의 학업수행 능력 평가는 아동의 학년 수준에 맞게 한국아동패널 연구진이 개발한 문항으로 모든 교과를 측정하였다. 평가 방법은 과목별 하위 항목을 초등교과 수준 목표에 따라 5점 Llikert 척도[‘하위 20% 이내(1점)’ - ‘상위 20% 이내(5점)]를 사용하여 평가하였다(Table 3, Appendix 2). 이러한 범주화 점수에 대한 종단평가를 위해 이번 연구에서는 5점 척도 개별 문항의 합계 점수를 구하고 이를 다시 100점 만점으로 환산하여 사용하였다.
연구절차이번 연구에 사용된 학업 능력 검사는 유치원 시기인 7차년도(2014년)에 대상자의 육아지원기관 담임교사를 대상으로, 그리고 학업수행 능력은 패널 대상자들이 초등학교에 입학한 8차년도(2015년)부터 11차년도(2018년)까지 매년 진행된 검사로 학교 담임 교사를 대상 조사로 진행되었다. 학업 능력과 학업수행 능력은 웹(web) 조사 방법을 사용하였으며 절차상에 있어 면접원이 우선 아동 부모의 동의를 얻어 담임 교사에게 연락을 하고, 조사 참여를 승낙하는 경우 6월부터 12월까지 대상 아동의 소속 학급 담임교사가 웹 조사를 통해 대상 아동의 학업수행 능력 결과에 대해 응답하는 방식으로 진행하였다.
이번 연구의 목표는 학령전 언어와 문해 능력이 초등학교 입학 후에 국어와 수학 학업수행 능력에 어떻게 영향을 미치며, 그리고 국어와 수학 학업 능력의 잠재성장 정도를 살펴보고, 국어(수학) 능력이 수학(국어)수행 능력에 어느정도 영향을 미치는 지를 살펴보는 것이다. 이에 한국아동패널에서 2014년(6세)부터 2018년(10세, 초등학교 4학년)까지 진행한 국어와 수학 학업(수행) 능력 종단연구 데이터를 제공받아 척도를 동일하게 하여 분석하였다.
자료분석수집된 자료는 IBM SPSS 21.0 프로그램과 AMOS 22.0 프로그램을 사용하여 분석하였다. 초등학생의 학업수행 능력 변화에 영향을 미치는 학업(수행) 능력(언어 및 문해 능력, 수리적 사고, 초등학교 1-4학년 때까지의 국어와 수학 학업수행 능력)을 탐색하기 위해 일변량과 다변량 잠재성장모델링분석(Latent growth curve analysis, LGCA)을 활용하였다.
잠재성장모델링은 개인내 모형(within subject model)과 개인 간모형(between subject model)으로 구성되며, 반복측정된 변인의 변화추이를 초기상태 및 변화율의 함수로 모형화하고, 추정된 잠재 성장 모수치(초기상태 및 변화율) 간의 잠재변인 회귀분석을 통해 변인 간의 변화 양상의 연관성을 분석하는 방법이다. 이번 연구에서는 유치원에서 초등학교 4학년 때까지의 학업(수행) 능력(언어 및 국어 학업 능력, 수리적 사고 및 수학 학업 능력)이 시간 경과에 따라 어떠한 변화 양상을 가지는지를 분석하기 위해 조건 선형 성장모형과 비선형 성장모형을 설정하고 적합도를 비교하였다. 선형 및 비선형 모형의 적합도 평가는 영가설이 기각되기 쉽고 표본크기에 민감한 χ2 과 함께 적합도 지수(TLI, CFI, RMSEA)를 사용하였다. 일반적으로 모형의 적합성 판단 기준은 χ2 통계량이 유의수준 .05 이상, TLI, CFI는 .90 이상, RMSEA는 .06 이하이면 모델의 적합도가 좋은 것으로 본다. 이 연구에서는 결측치를 제거하고(Listwise) 다섯 시점에서 연속적으로 측정된 자료를 활용하였으므로 모형의 추정방법으로 최대우도법(ML)을 사용하였다.
그리고 이후에는 초등학교 4학년 때의 수학(국어) 능력에 영향을 미치는 학년별 국어와 수학 학업(수행) 능력이 있는지 그리고 영향 변수가 얼마만큼의 예측성을 가지는지를 다중회귀분석을 통해 살펴보았다.
연구결과연구결과1: 기술통계 및 상관분석관측 개별시점에서의 과제 수행 정도의 경향을 알아보기 위해 평균과 표준편차 값을 산출하였고, 그 결과는 Table 4에 제시하였다. 첫 번째 분석에서는 각 개별 연령 시점에서의 학업 능력 관계를 상관분석을 통해 살펴보았다. 총 10개 변수의 상관분석 결과도 Table 4에 제시하였다. 평가 결과 대부분의 국어와 수학 학업 능력이 서로 상관도가 높게 나타났지만 학령전 유치원 시기의 언어 및 문해 능력은 초등학교 3학년 시기의 수학 학업수행 능력과는 유의미한 상관이 없었다. 그리고 학령전 유치원 시기의 수학적 사고 능력은 초등학교 3학년 시기의 국어와 수학 학업 능력과는 유의미한 상관이 없는 것으로 나타났다. 그리고 연령별 국어와 수학 학업 능력 상관이 다른 연령의 결과와 유의미한 상관이 있기는 했지만, 유독 같은 학년에서의 국어와 수학 학업 능력 점수와의 상관은 .57이상으로 매우 높게 나타났다(Table 4).
연구결과2: 잠재성장모델 분석모형 적합도언어 및 국어 학업능력(학령전 언어 및 문해 학업 능력, 초등학교 1-4학년까지의 국어 학업수행 능력)과 수학 학업 능력(학령전 수리적 사고, 초등학교 1-4학년까지의 수학 학업수행 능력)의 잠재성장 변화 모델을 구분하여(Univariate Latent Growth Curve Model), 시간 변화에 따라 발달 양상을 살펴보았다. 잠재성장모형은 조건 선형 변화모형과 조건 비선형 변화모형을 구분하여 분석한 결과 조건 비선형 변화모형이 더 적합한 것으로 판단되었다. 즉, 조건 비선형 변화모형의 적합도를 평가한 결과 TLI, CFI가 .88과 .72로 .9에 유사한 것으로 나타났다. 즉, TLI, CFI 지수가 모형 적합도 기준에 상응하는 것으로 나타나 본 연구의 측정 모형을 만족할 만한 수준으로 판단하였다(Table 5).
그리고 언어 및 국어 학업 능력(학령전 언어 및 문해 학업 능력, 초등학교 1-4학년까지의 국어 학업수행 능력)과 수학 학업 능력(학령전 수리적 사고, 초등학교 1-4학년까지의 수학 학업수행 능력)의 관계에 대한 잠재성장 변화 모델 분석을 통해 시간 변화에 따라 언어와 수학 학업 능력의 발달 양상의 관계(Multivariate Latent Growth Curve Model)를 살펴보았다. 다변량 잠재성장모형 조건 비선형 관계 변화모형의 적합도를 평가한 결과 카이점정의 유의확률 p값이 .05이하였는데, 이것은 모델에 포함된 대상자의 수가 133명으로 적은 인원수라는 한계에 의한 영향으로 보여 진다. 이외 TLI, CFI이 .56과 .64로 .9에 미치지 못하여 모형 적합도가 높은 편은 아니었다 (Table 5). 이에 먼저 일변량 잠재성장모형을 Figures 2, 3에 제시하고 이후 다변량 잠재성장모형은 Figure 4에 제시하였다.
성장모형 분석언어 및 국어 수행 능력의 상수항(ICEPT)은 74.27이고, 기울기(SLOPE)는 10.55, 2차식의 기울기(QUAD)는 -6.82이다(Figure 2). 상수와 기울기 모두 유의확률(p)이 .001보다 작기 때문에 상수항과 1차식과 2차식 기울기 모두가 통계적으로 유의미하다. 하지만 모델 적합도에서 1차식 모형의 적합도가 모형 적합도 수치에 만족할 수준에 미치지 못하였다. 언어 및 국어수행 능력 성장모형은 2차식 기술기를 적용한 비선형의 약간 곡선의 성장을 보이는 것으로 판단된다. 5개의 언어 및 국어수행 능력 성장모형의 함수식을 적용하여, 예측평균 값(Implied mean) 변화를 그래프로 나타나면 Figure 1과 같다. 국어 학업수행 능력은 초등학교 4학년을 기준으로 점수의 상승 정도가 하락하는 경향을 보였으며 그 정도는 -6.82점으로 나타났다. 그리고 수학 학업수행 능력도 초등학교 4학년을 기준으로 점수가 하락하는 성향을 보였으며 그 정도는 -10.26점으로 나타났다(Figure 1).
국어 학업수행 능력 성장모형은 2차식 기술기를 적용한 비선형의 약간 곡선의 성장을 보이는 것으로 나타났다. 5개의 국어와 수학 학업수행 능력 성장모형의 함수식을 적용하여, 예측평균 값(Implied mean) 변화를 그래프로 나타나면 Figure 1과 같다. 상수항과 기울기 모두 유의확률(p)이 .001보다 작기 때문에 상수항과 1차식과 2차식 기울기 모두가 통계적으로 유의미하다. 하지만 모델 적합도에서 1차식 모형의 적합도가 모형적합도 수치에 만족할 수준에 미치지 못하였고 2차식 모형은 모형 적합도가 만족할 수준이었다(Table 5).
일변량 잠재성장모델국어와 수학 학업 능력의 발달을 각각 살펴보기 위하여 국어와 수학 변수 각각에 대한 일변량 잠재성장모델 분석을 실시하였다. 이러한 잠재성장모델은 시간변화에 따른 자료의 변화의 크기를 종단으로 살펴보는 방법이다. 즉, 개별 아동의 성장곡선을 추정하는 것을 목표로 하는 것으로 실측 데이터인 관측변수는 사각형으로 제시하여 대상자 아동 집단 내의 성장 변화를 측정할 수 있다. 원형으로 표시되는 상수(intercept)는 개별 대상자들 본연의 일반적 능력 또는 인지적 능력을 의미한다. 또한 기울기(slope)는 시간 변화에 따른 평균 변화 값을 의미한다. 즉, 상수와 기울기는 잠재변수로 작용하고 있으며 원형으로 표현된다. 이번 연구에서는 유치원 만 6세 첫 번째 시점부터 초등학교 4학년 다섯 번째 시점까지의 자료의 기울기를 추정하였다.
먼저 국어 학업수행 능력 잠재성장 변화를 살펴보면 상수와 기울기 값의 유의미한 공분산(covariance)은 없었다. 즉, 개별 아동의 일반적 능력 또는 인지적 능력이 학업 능력 성장률에 영향을 미치는 것은 아닌 것으로 볼 수 있다. 그리고 국어 상수(intercept)의 평균(M = 74.27, SE =1.25, p<.001)과 변량(M = 72.9, SE = 27.67, p<.01) 모두가 유의미하였다. 이러한 값은 대상자 아동의 국어 학업수행 개별 능력이 0점이 아닌 평균 수준이며, 개별 아동의 평균은 서로 유의미하게 다르다는 것을 의미한다. 국어 학업수행 능력 변화의 기울기(slope) 평균(M =10.55, SE =1.22, p<.001)은 유의미하였으나, 변량(M =12.20, SE = 29.09, p=.67)은 유의미한 차이를 보이지 않았다. 이는 국어 학업수행 능력은 시간 변화에 따라 유의미한 변화가 이루어졌으나, 이러한 변화가 개별 아동별로 차이가 유의미하지는 않았다는 것을 의미한다. 그리고 국어 학업수행 능력 변화의 비선형모형(QUAD) 기울기 잠재변수의 평균(M = -1.93, SE = .28, p<.001)은 유의미하였지만, 변량 (M = -.05, SE =1.59, p=.97)은 유의미하지 않았다. 이러한 결과는 국어 학업수행 능력은 시간 변화에 따라 유의미한 2차식의 변화가 나타났으며, 이러한 2차식의 변화는 개별 아동별로 유의미한 차이가 나타나지 않았으며 유사한 변화가 나타났다는 것을 의미한다(Figure 2).
두 번째로 수학 학업수행 능력 잠재성장 변화를 살펴보면 상수와 기울기 값(SLOPE, QUAD)의 유의미한 공분산(covariance)이 나타났다. 즉, 개별 아동의 일반적 능력 또는 인지적 능력이 학업 능력 성장률에 영향을 미치는 것으로 볼 수 있다. 그리고 수학 상수(intercept)의 평균(M=69.79, SE =1.41, p<.001)과 변량(M=123.74, SE = 34.20, p<.001) 모두가 유의미하였다. 이러한 값은 대상자 아동의 수학 학업수행 개별 능력이 0점이 아닌 평균 수준이며, 개별 아동의 평균은 서로 유의미하게 다르다는 것을 의미한다. 수학 학업수행 능력 변화의 기울기(slope) 평균(M=16.36, SE=1.42, p<.001) 과 변량(M = 75.57, SE = 36.92, p=.05) 모두가 유의미한 차이를 보였다. 이는 수학 학업수행 능력은 시간 변화에 따라 유의미한 변화가 나타났으며, 이러한 변화가 개별 아동별로 유의한 차이가 있었다는 것을 의미한다. 그리고 수학 학업수행 능력 변화의 비선형모형(QUAD) 기울기 잠재변수의 평균(M = -3.09, SE = .30, p<.001)은 유의미하였지만, 변량(M = .99, SE =1.76, p=.57)은 유의미하지 않았다. 이러한 결과는 수학 학업수행 능력은 시간 변화에 따라 유의미한 2차식의 변화가 나타났으며, 이러한 2차식의 변화는 개별 아동별로 유의미한 차이가 나타나지 않고 유사한 변화가 나타났다는 것을 의미한다(Figure 3).
다변량 잠재성장모델국어와 수학 학업 능력 발달모델 간 상호관계를 살펴보기 위하여, 위의 국어와 수학 일변량 잠재성장모델 변량의 상수항과 기울기의 관계변화를 측정하는 다변량 잠재성장모델을 실시하였다(Figure 4). 상수-기울기의 상관관계를 분석한 결과 수학 학업수행 능력 기본값(intercept)은 국어 학업수행 능력 기울기(slope) 변화에 유의미한 영향을 미치기는 하였지만(p<.01), 다른 잠재변수들과의 관계보다는 그 유의미성이 상대적으로 낮게 평가되었다. 그리고 국어 학업수행 능력 기본값(intercept)은 수학 학업수행 능력 상수와 기울 모두에 유의미한 영향을 미치는 변수로 작용하였다. 그리고 국어와 수학 학업수행 능력의 기울기는 서로에게 유의미한 영향을 미치고 있었다. 즉, 국어 학업수행 능력의 진전은 수학 학업수행 능력에도 진전을 보이는 경향이 나타남을 의미한다(Figure 4).
연구결과3: 초등학교 4학년 수학과 국어 학업수행 능력 예측 변수초등학교 4학년 국어 학업수행 능력에 대한 중다회귀분석초등학교 4학년의 국어와 수학 학업수행 능력에 대한 중다회귀분석 분산분석표는 Table 6과 같다. 우선 초등학교 4학년의 국어 수행평가점수에 대한 중다회귀분석에서도 아홉 개의 독립 변수(유치원 시기의 언어 및 문해 능력과 수리적 사고, 초등학교 1학년부터 3학년까지의 국어와 수학 학업수행 능력, 초등학교 4학년의 수학 학업수행 능력)로 초등학교 4학년의 국어 학업 능력을 측정하는 모형에 대한 통계적 유의성을 검정하였다. 연구결과, 7개 변수(상수, 유치원 시기의 언어 및 문해 능력과 수리적 사고, 초등학교 1학년 때 국어와 수학 학업수행 능력, 초등학교 3학년 때의 수학 학업수행 능력)는 유의하지 않아 제외되었다. 그 외 초등학교 때의 4개 변수(초등학교 2학년 때의 국어와 수학, 초등학교 3학년 때의 국어 학업수행 능력, 그리고 초등학교 4학년의 수학 학업수행 능력)는 모형에 포함되었다(Table 7). 포함된 모형의 F 통계값은 23.97, 유의확률은 .000으로 모형에 포함된 독립변수는 유의수준 .001에서 초등학교 4학년 국어 학업수행 능력을 유의하게 설명하고 있으며, 만족도 총량변화의 64%(수정 결정계수에 의하면 61%)가 모형에 포함된 독립변수에 의해 설명되고 있다(Table 6). 개별 독립변수의 종속변수에 대한 기여도와 통계적 유의성을 검정한 결과, 유의수준 .05에서 초등학교 4학년 국어 학업수행 능력에 유의하게 영향을 미치는 독립변수는 초등학교 4학년의 수학 학업수행 능력(t=9.27, p=.000), 초등학교 3학년 때의 국어 학업수행 능력(t=3.29, p=.001), 초등학교 2학년 때의 국어 학업수행 능력(t=2.51, p=.013), 초등학교 2학년 때의 수학 학업수행 눙력(t=-2.48, p=.014)이다. 그리고 독립변수의 상대적 기여도를 나타내는 표준화 계수에 의하면 초등학교 4학년 때의 수학, 3학년 때의 국어, 2학년 때의 국어, 수학 학업수행 능력의 순으로 초등학교 4학년 때의 국어 학업수행 능력에 영향을 미치고 있다(Table 7).
초등학교 4학년 수학 학업수행 능력에 대한 중다회귀분석수학 학업수행 능력에 대한 중다회귀분석에서는 아홉 개의 독립 변수(유치원 시기의 언어 및 문해 능력과 수리적 사고, 초등학교 1학년부터 3학년까지의 국어와 수학 학업수행 능력, 초등학교 4학년의 국어 학업수행 능력)로 초등학교 4학년의 수학 학업 능력을 측정하는 모형에 대한 통계적 유의성 검정을 실시하였다. 연구결과, 9개 독립변수 중 6개 변수(유치원 시기의 언어 및 문해 능력과 수리적 사고, 초등학교 1학년 때 국어, 초등학교 2학년 때의 국어와 수학, 초등학교 3학년 때의 국어 학업수행 능력)는 유의하지 않아 제외되었다. 그 외 초등학교 때의 4개 변수(상수, 1학년 때의 수학, 초등학교 3학년 때의 수학, 그리고 초등학교 4학년의 국어 학업수행 능력)은 모형에 포함되었다(Table 7). 포함된 모형의 F 통계값은 22.26, 유의확률은 .000으로 모형에 포함된 독립변수는 유의수준 .001에서 초등학교 4학년 수학 학업수행 능력을 유의하게 설명하고 있으며, 만족도 총량변화의 62%(수정 결정계수에 의하면 59%)가 모형에 포함된 독립변수에 의해 설명되고 있다(Table 6). 개별 독립 변수의 종속변수에 대한 기여도와 통계적 유의성을 검정한 결과, 유의수준 .05에서 초등학교 4학년 수학 학업수행 능력에 유의하게 영향을 미치는 독립변수는 초등학교 4학년의 국어 학업수행 능력(t=9.27, p=.000), 초등학교 3학년 때의 수학 학업수행 능력(t=2.23, p=.028), 초등학교 1학년 때의 수학 학업수행 능력(t=2.07, p=.041)이다. 그리고 독립변수의 상대적 기여도를 나타내는 표준화 계수에 의하면 초등학교 4학년 때의 국어, 3학년 때의 수학, 1학년 때의 수학 학업수행 능력의 순으로 초등학교 4학년 때의 수학 학업수행 능력에 영향을 미치고 있다(Table 7).
논의 및 결론본 연구는 일반 아동을 대상으로 6세 유아 시기부터 10세 초등학교 4학년 때까지의 국어와 수학 학업수행 능력의 관련성과 연령 변화에 따른 잠재성장을 살펴보았다. 그리고 마지막으로 초등학교 4학년 때의 국어와 수학 학업수행 능력을 예측하는 전 학년 국어와 수학 학업수행 능력은 구체적으로 어떠한 부분인지를 살펴보았다. 그 주요 연구결과들을 중심으로 논의하면 다음과 같다.
첫째, 각 개별 연령 시점에서의 학업 능력 관계를 상관분석을 통해 살펴보았다. 분석 결과 대부분의 국어와 수학 학업 능력 변수들은 서로 상관도가 높게 나타났다. 하지만 6세 유치원 시기의 언어 및 문해 능력은 초등학교 3학년 시기의 수학 학업수행 능력과는 유의미한 상관이 없었고, 유치원 시기의 수학적 사고 능력은 초등학교 3학년 시기의 국어와 수학 학업 능력과는 유의미한 상관이 없는 것으로 나타났다. 연구결과, 초등학교 3학년 시기의 학업 능력은 대상자들의 유아기의 기본적 학업 능력과는 유의미한 관련이 없는 것을 알 수 있었다. 이러한 결과를 좀 더 세부적으로 살펴보기 위해 연구과제에서 초등학교 3학년의 국어와 수학 학업수행 능력 평가 문항을 살펴보면 이러한 결과를 예상할 수 있다. 초등학교 3학년때 국어 학업수행 능력 평가 문항에는 1-2학년 시기 때 국어 평가가 듣기, 말하기, 읽기와 쓰기 정도를 본 것과는 달리 글을 읽고 중심 내용을 파악하는 능력과 말하기 능력, 그리고 문단들을 이해하고 글을 쓰는 능력을 평가하고 있다. 그러므로 기본적인 읽기와 쓰기 능력이 완성되어 있어야 높은 수행을 보일 수 있다. 이러한 평가 요소들은 유아기의 언어 및 문해 능력 수준을 뛰어넘는 높은 수준의 국어 능력이 요구된다. 그리고 초등학교 3학년 때 수학은 연산(arithmetic)의 자리수가 3자리 수 이상으로 증가하며 곱셈과 나눗셈 연산, 분수와 소수의 이해, 시간과 길이, 들이와 무게의 단위를 이해하고 측정하는 계산 능력을 평가하고 있다. 이것은 초등학교 1학년과 2학년 때 덧셈과 뺄셈, 도형의 이해 능력을 측정했던 문제들과는 다른 추상적 상징 능력이 더욱 요구되는 요소들이다. 그러므로 유아기의 수리적 사고 능력 이외의 학습을 통한 이해가 필요한 부분이며 이러한 부분이 유아기의 학업 능력과 초등학교 3학년 학업 능력과의 상관에 영향을 미친 것으로 볼 수 있다.
둘째, 연령별 국어와 수학 학업 능력 상관이 다른 연령의 결과와 유의미한 상관이 있기는 했지만, 유독 같은 학년에서의 국어와 수학 학업 능력 점수와의 상관은 .57이상으로 매우 높게 나타났다. 즉 국어와 수학의 상관관계는 같은 연령의 수행 능력 간에 높은 상관이 있다는 것을 확인하였다. 이러한 현상은 초등학교 수학 문장제와 관련하여 해석할 수 있다(Dowker, 2008). 즉, 계산에 현저한 장애를 갖는 계산장애(dyscalculia, arithmetical difficulty)가 있는 대상자가 아니라면 기본적인 수학 언어(더하다, 빼다, 주다, 남다, 주다, 삼각형, 사각형, 원, 깊이, 넓이 등)와 국어 문장의 의미와 문법적 이해 능력이 있어야 수학문제 풀이가 가능하다(Toll & Van Luit, 2014). 이러한 측면에서 살펴보면 동일 연령대의 국어와 수학 학업 수행 능력 간의 상관이 가장 높다는 것은 이해 가능하다.
셋째, 국어에 대한 일변량 잠재성장모델 분석을 실시한 결과, 국어 학업수행 능력 잠재성장 변화는 상수와 기울기 값의 유의미한 공분산(covariance)은 없었다. 이러한 결과를 통해, 개별 일반 아동의 일반적 능력 또는 인지적 능력은 국어 학업수행 능력 성장률에 유의미한 영향을 미치지 않는다고 볼 수 있다. 이러한 값은 대상자 아동의 국어 학업수행 개별 능력이 0점이 아닌 평균 수준이며, 개별 아동의 평균은 서로 유의미하게 다르다는 것을 의미한다. 그리고 일반 아동의 국어 학업수행 능력은 아동 개인의 기본 능력이 국어 학업수행 능력 성장에 유의미한 영향을 미치지 않기에, 학년별 과제와 학습요소에 어느정도 집중력을 가지고 학습하는지에 따라, 개별 대상자의 국어 학업수행 능력 결과가 달라진다고 볼 수 있다.
넷째, 일변량 잠재성장모델 분석에서 국어 학업수행 능력 변화 기울기(slope) 평균(M =10.55, SE =1.22, p<.001)은 유의미하였으나, 변량(M =12.20, SE = 29.09, p=.67)은 유의미한 차이를 보이지 않았다. 그리고 국어 학업수행 능력 변화의 비선형모형(QUAD) 기울기 잠재변수의 평균(M = -1.93, SE = .28, p<.001)은 유의미하였지만, 변량 (M = -.05, SE =1.59, p=.97)은 유의미하지 않았다. 이러한 결과는 국어 학업수행 능력은 시간 변화에 따라 유의미한 2차식의 변화가 나타났으며, 이러한 2차식의 변화는 개별 아동별로 유의미한 차이가 나타나지 않았으며 유사한 변화가 나타났다는 것을 의미한다. 이는 국어 학업수행 능력은 시간 변화에 따라 평균 학업 수행 능력은 유의미한 변화가 곡선형 변화로 나타나고 있었지만, 개별 아동별로 살펴보았을 때는 그 차이가 유의미하지는 않았다는 것을 의미한다. 그러므로 국어 학업수행 능력 평균 변화에서 개별 아동의 수행능력이 유사한 패턴으로 진행되었음을 알 수 있다. 유아기의 언어와 문해 능력이 높았던 아동은 이후 초등학교 입학 이후에도 국어 학업수행 능력이 높았으며 그 역도 가능하다는 것으로 해석할 수 있다.
다섯째, 수학 학업수행 능력 잠재성장 변화를 살펴보면 상수와 기울기 값(SLOPE, QUAD)의 유의미한 공분산(covariance)이 나타났다. 즉, 개별 아동의 일반적 능력 또는 인지적 능력이 학업 능력 성장률에 영향을 미치는 것으로 볼 수 있다. 이는 국어 학업수행 능력과는 다른 결과이다. 국어의 경우에는 상수와 기울기는 유의미한 공분산이 없었다. 즉, 국어는 개별 대상자의 기본 능력이 국어 학업수행 능력 변화에 영향을 미치지 않았지만 수학의 경우는 국어와 달리 개별 대상자의 기본 능력이 수학 학업수행 능력 변화에 영향을 미치는 것으로 나타났다. 즉, 수학은 기본적 개별 대상자의 역량이 수행 능력 변화에 중요한 부분으로 작용하고 있다고 볼 수 있다. 그러므로 국어보다는 수학 학업 능력은 타고난 기본적 인지 능력이 요구되는 과목으로 해석할 수 있다. 그렇다면 인지 능력에 제한이 있는 대상자들의 경우는 수학 학업 능력에 제한이 있을 가능성이 높다.
여섯째, 학업수행 능력 잠재성장 변화에서 수학 상수의 평균(M=69.79, SE =1.41, p<.001)과 변량(M =123.74, SE = 34.20, p<.001) 모두가 유의미하였다. 이러한 값은 대상자 아동의 수학 학업수행 개별 능력이 0점이 아닌 평균 수준이며, 개별 아동의 평균은 서로 유의미하게 다르다는 것을 의미한다. 그리고 수학 학업수행 능력 변화의 기울기 평균(M=16.36, SE =1.42, p<.001)과 변량(M=75.57, SE = 36.92, p=.05) 모두가 유의미한 차이를 보였다. 그리고 수학 학업수행 능력 변화의 비선형모형(QUAD) 기울기 잠재변수의 평균 (M = -3.09, SE = .30, p<.001)은 유의미하였지만, 변량(M = .99, SE = 1.76, p=.57)은 유의미하지 않았다. 이러한 결과는 수학 학업수행 능력은 시간 변화에 따라 유의미한 2차식의 변화가 나타났으며, 이러한 2차식의 변화는 개별 아동별로 유의미한 차이가 나타나지 않고 유사한 변화가 나타났다는 것을 의미한다(Figure 3). 그리고 수학 학업수행 능력은 시간 변화에 따라 유의미한 변화가 나타났으며, 이러한 변화가 개별 아동별로 유의한 차이가 있었다는 것을 의미한다. 이러한 수학 학업수행 능력 잠재성장모델 분석 결과는 국어 학업수행 능력 잠재성장모델과는 큰 차이를 보인다고 볼 수 있다. 국어와는 달리 수학 학업수행 능력은 개별 대상자의 기본 인지 능력이 수행 변화에 중요 요인으로 작용하고 있기도 하며, 개별 아동의 수학 학업수행 능력의 평균 차이가 국어보다는 유의미하게 차이를 보인다는 것이다. 그러므로 국어에 비하여 수학의 학업수행 능력이 개별 아동별로 큰 차이를 보이는 것으로 판단된다. 유아기에 수리적 사고 학업 능력이 낮았던 아동도 초등학교 시기에 수학 학업수행 능력이 높아질 수도 있으며 그 반대의 경우도 가능하다는 것이다. 종합하여 해석하면 수학은 기본적인 인지 능력과 개인의 학업 역량 모두가 학업수행에 영향을 미치는 과목이라고 해석할 수 있다.
일곱째, 국어와 수학 학업 능력 발달모델 간 상호관계를 살펴보기 위하여, 위의 국어와 수학 일변량 잠재성장모델 변량의 상수항과 기울기의 관계변화를 측정하는 다변량 잠재성장모델을 실시하였다(Figure 4). 상수-기울기의 상관관계를 분석한 결과 수학 학업 수행 능력 기본값(intercept)은 국어 학업수행 능력 기울기(slope) 변화에 유의미한 영향을 미치기는 하였지만(p<.01), 다른 잠재변수들과의 관계보다는 그 유의미성이 상대적으로 낮게 평가되었다. 그리고 국어 학업수행 능력 기본값(intercept)은 수학 학업수행 능력 상수와 기울기 모두에 유의미한 영향을 미치는 변수로 작용하 였다. 하지만 수학 학업수행 능력의 기본값(intercept)은 국어 학업 수행 능력의 기본값과 유의미한 상호관계가 있을 뿐 국어 학업수행 능력 기울기와는 유의미한 상호관계가 나타나지 않았다. 그리고 국어와 수학 학업수행 능력의 기울기는 서로에게 유의미한 영향을 미치고 있었다. 이러한 결과를 해석해보면, 국어 학업수행 능력의 기본적 능력이 수학 학업 능력의 기본 능력과 발달 모두에 유의미한 영향을 미치고 있는 것과는 달리, 수학 학업수행 능력은 국어 기본적 학업 능력에는 영향을 미치지만 국어 학업수행 능력 발달에 유의미한 영향을 미치지는 않는 것으로 볼 수 있다. 그러므로 수학 학업수행을 위해서는 국어 기본 능력이 더욱 요구된다는 것을 확인하였다.
이상의 연구결과를 통해, 본 연구에서 시사하는 바는 다음과 같다. 첫째, 초등학교 3학년부터는 국어와 수학 학업수행 평가 영역이 이전 학년과는 많은 차이를 보인다. 초등학교 1학년과 2학년 시기에 읽기와 쓰기 기본 문해 능력이 완성되어 있어야 하며 수학 학업수행 능력 향상을 위해서는 기본적인 연산(더하기, 빼기, 곱하기, 나누기) 개념이 1학년과 2학년 시기에 잘 형성되어 있어야 한다. 수학은 기본개념에 대한 이해가 수학 학업수행 능력 변화에 유의미한 영향을 미치는 것으로 나타났다. 그러므로 기본 연산학습을 이해시킬 수 있는 교수법에 대한 개발과 교수자의 역량이 요구된다. 그리고 이러한 부분에 있어 언어를 이해하고 문법적 담론을 해석해 내는 것은 아주 중요한 부분을 차지하고 있다. 그러므로 학령기 아동 중 언어 발달에 지체를 보이거나 장애가 있는 대상자들에게는 조금 더 수학적 언어와 수학적 담론의 문장을 읽고 이해하는 부분에 대한 추가 지원이 요구된다. 둘째, 국어와 수학 학업수행 능력이 서로 유의미한 영향을 미치고 있음을 확인하였다(Toll & Van Luit, 2014). 그러므로 초등학교의 모든 과목이 통합적 요소로 학습이 되기는 하지만 특히 국어와 수학 학습에 통합적 요인이 필요함을 확인할 수 있었다. 셋째, 국어와 수학은 서로 영향을 미치기는 하지만 수학의 경우는 학업수행 능력 결과에 개별 아동의 인지 능력이 국어에 비하여 유의미하게 작용하고 있음을 확인하였다. 그러므로 초등학교 수학 학업수행 능력 발달을 위해서는 인지적 역량을 확대할 수 있는 부분이 유아기 시기부터 잘 준비되어야 할 것으로 보인다(Toll & Van Luit, 2012). 이에 학령전 아동 중 언어발달지체와 언어발달장애가 있는 아동에게는 학령기를 대비한 인지적 역량 지원이 계속적으로 진행되어야 할 것으로 보인다. 넷째, 국어와 수학은 서로 유의미한 영향을 미치며 발달하고 있었다. 특히 국어 학업 수행 기본 능력은 수학 학업의 기본 능력과 학업 능력 변화 모두에 유의미한 영향을 미치고 있음을 확인하였다. 이러한 결과는 수학 문장제의 언급을 통해 국어 능력이 수학 학업 능력의 기초라는 것은 많이 언급된 사실이다. 하지만 이러한 언급을 이번 연구를 통해 실제 데이터 분석으로 결과를 제시하였다는 것은 큰 의미를 가진다. 다섯째, 국어는 기초 학문으로서 수학 학습 발달에 유의미한 영향을 미치고 있음을 이번 연구 분석 결과를 통해 실제적으로 확인하였다. 그러므로 학교 현장에서의 국어 학습 지체 또는 언어발달에 문제를 보이는 대상자들에게는 기초학습을 위한 언어학습 지원이 학교내에서 더욱 요구된다. 언어와 수학은 학교 밖 생활활동에서 가장 요구되는 기초 학문이다. 그러므로 기초학력 지원이 학교 안에서 전문가를 통해 이루어지는 것은 이후 경제인력양성을 위한 추가 지원을 줄이는 효과로 작용할 것이다.
이에 본 연구결과를 토대로 본 연구가 갖는 제한점을 밝히며 후속 연구에 대한 제언을 제시하면 다음과 같다. 이번 연구의 기본 데이터에는 초등학교 1학년부터 초등학교 6학년까지의 데이터가 존재한다. 하지만 대상자 아동이 7년간의 연구에 모두 참여한 대상자는 초기 대상자 수에 비하여 매우 적었다. 이에 종단연구의 이점을 살리고자 하는 연구자의 의견에 따라 초등학교 4학년까지의 데이터만을 분석하였다는 아쉬움이 있다. 이에 추후 연구에서는 종단 연구가 아닌 대상자 연령별로 학업수행 능력을 횡단으로 비교하는 것도 의미가 있을 것으로 보인다. 그리고 이러한 경우는 초등학교 전 학년의 학업 능력을 비교해 볼 수 있다는 장점이 있다. 이때의 연구결과를 이번 연구의 종단연구결과와 비교해 보는 것도 유의미할 것으로 보인다. 둘째, 종단연구의 경우는 모든 대상자가 참여할 수는 없으며 일부 데이터나 대상자의 손실이 있을 수 있다. 하지만 특정 해에 대상자들의 참여가 매우 낮은 이유 또는 참여를 계속 진행한 대상자들의 공통적인 속성이 있을지에 대한 의아함을 가져보았다. 그러므로 다음 연구에서는 연구에 계속적인 참여를 한 대상자들의 특성을 살펴보는 것도 필요할 것으로 보인다. 셋째, 이번 연구는 한국아동패널의 종단연구를 분석한 것으로 국어와 수학 학업수행 능력 문항이 다양하지 못했다는 것에 아쉬움이 있다. 국어와 수학도 그 영역별로 구분하면 다양하다. 그러므로 국어와 수학을 다양한 영역으로 구분하여 분석하여 그 관계성을 살펴볼 수 있었다면 더 의미 있는 연구가 되었을 수도 있다. 이에 추가 연구에서는 국어와 수학의 평가 항목을 다양화해서 항목별 발달 관계를 살펴보면 좋을 것이다. 마지막으로 언어발달장애 대상자들의 언어와 수학 학습의 관계를 살펴본 몇몇 국외 연구에서는 언어발달의 문제가 있는 학령기 대상자들은 일반 아동에 비하여 수학 학습 능력이 유의미하게 낮은 것을 확인하였다(Arvedson, 2002; Cowan et al., 2008; Fazio, 1999). 이에 국내에서도 국어와 수학 학업 능력이 낮은 기초학력 미달 대상자만으로 학업수행의 변화를 살펴보는 연구가 추가되었음 한다. 본 연구 대상자 중에는 기초학력 미달 대상자가 매우 극소수였다. 그리고 이들 대상자들이 종단연구에 참여하는 비율은 매우 낮았으므로 분석을 하는 것은 어려웠다. 그러므로 이들 대상자만을 모집할 수 있는 여건에서 학습 능력의 변화를 분석하여 보는 것은 학령기 아동의 언어와 수학 학습 지원을 위한 기초 연구가 될 것으로 보인다.
Figure 1.Implied mean growth trajectories in language and math academic ability.
E1 = the first grade of elementary school; E2 = the second grade of elementary school; E3 = the third grade of elementary school; E4 = the fourth grade of elementary school; Lang.= Language.

Figure 2.The univariate latent growth model of the Korean academic performance.
K = Kinder; E1 = the first grade of elementary school; E2 = the second grade of elementary school; E3 = the third grade of elementary school; E4 = the fourth grade of elementary school.
**p < .001, ***p < .0000.
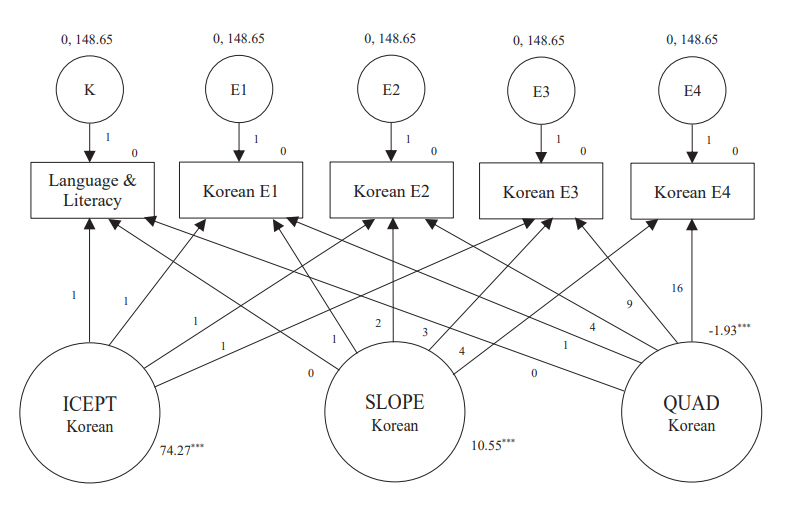
Figure 3.The univariate latent growth model of the mathematic academic performance.
K = Kinder; E1 = the first grade of elementary school; E2 = the second grade of elementary school; E3 = the third grade of elementary school; E4 = the fourth grade of elementary school.
*p < .05, **p < .001, ***p < .0000.
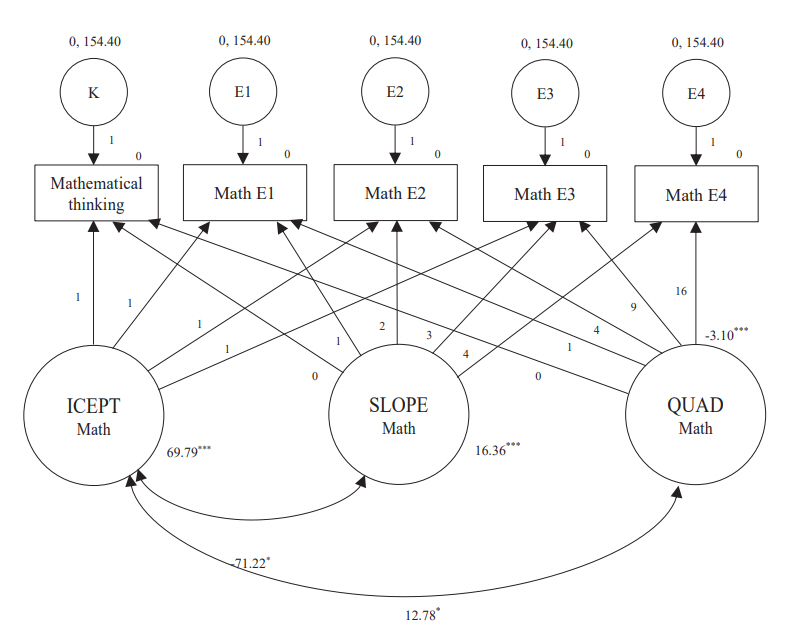
Figure 4.The multivariate growth model of the Korean and mathematic academic performance.
K = Kinder; E1 = the first grade of elementary school; E2= the second grade of elementary school; E3 = the third grade of elementary school; E4 = the fourth grade of elementary school.
*p < .05, ***p < .0000.
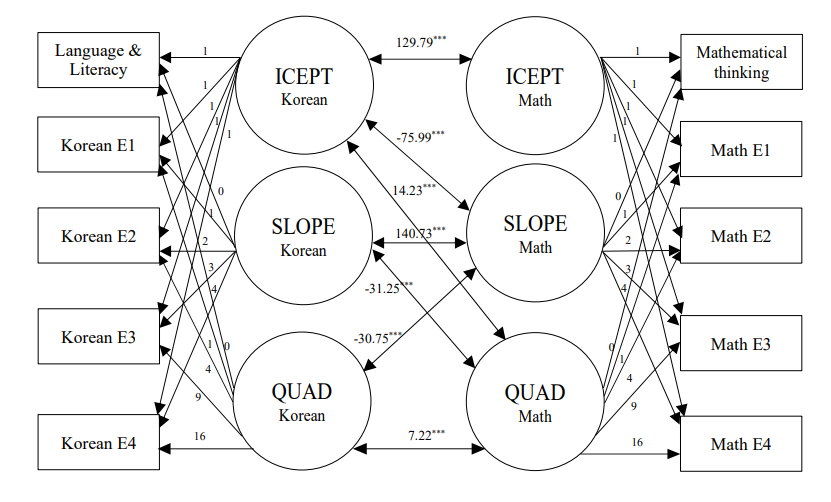
Table 1.Participants’ information (N=133)
Table 2.Items and scale of academic skills (language and literacy, mathematical thinking) Source=KICCE (Korea Institute of Child Care and Education, https://kicce.re.kr/panel); NICHD Study of Early Child Care and Youth Development: Phase II, 1995-1999 [United States] (ICPSR 21941) (http://www.icpsr.umich.edu/icpsrweb/ICPSR/studies/21941). B=Beginning; IP=In Progress; Int=Intermediate; NY=Not Yet; P=Proficient. Table 3.Academic performance questions items (Korean, math) Table 4.Descriptive statistics of and correlations among continuous study variables (N=133)
Table 5.Fit indices for univariate and multivariate latent growth models
Table 6.Analysis of variance
Table 7.Multiple regression analyses on scales of E4 (N=133)
REFERENCESArvedson, P. J. (2002). Young children with specific language impairment and their numerical cognition. Journal of Speech, Language, and Hearing Research, 45(5), 970–982.
Bideaud, J., Meljac, C., & Fischer, J. P. (1992). Pathways to number: children’s developing numerical abilities Hillsdale, NJ: Erlbaum.
Cowan, R., Donlan, C., Newton, E. J., & Lloyd, F. (2008). Number development and children with specific language impairment. In A. Dowker (Ed.), Mathematical difficulties: psychology and intervention (pp. 155–166). San Diego, CA: Academic Press.
In A. Dowker (Ed.), (2008). Mathematical difficulties: psychology and intervention San Diego, CA: Academic Press.
Ellis, S. A. T., Miles, T. R., & Wheeler, T. J. (2008). The performance of dyslexic and non-dyslexic boys at division sums. In A. Dowker (Ed.), Mathematical difficulties: psychology and intervention (pp. 167–180). San Diego, CA: Academic Press.
Fazio, B. B. (1996). Mathematical abilities of children with specific language impairment: a 2-year follow-up. Journal of Speech and Hearing Research, 39(4), 1–10.
Fazio, B. B. (1999). Arithmetic calculation, short-term memory, and language performance in children with specific language impairment: a 5-year follow-up. Journal of Speech, Language, and Hearing Research, 42(2), 420–431.
Gelman, R. (1997). Constructing and using conceptual competence. Cognitive Development, 12(3), 305–313.
Gersten, R., & Chard, D. (1999). Number sense: rethinking arithmetic instruction for students with mathematical disabilities. Journal of Speech Education, 33(1), 18–28.
Kleemans, T., Segers, E., & Verhoven, L. (2011). Cognitive and linguistic precursors to numeracy in kindergarten: evidence from first and second language learners. Learning and Individual Differences, 21(5), 555–561.
Koponen, T., Mononen, R., Räsänenn, P., & Ahonen, T. (2006). Basic numeracy in children with specific language impairment: heterogeneity and connections to language. Journal of Speech, Language, and Hearing Research, 49(1), 58–73.
Mazzocco, M. M. M. (2005). Challenges in identifying target skills for math disability screening and intervention. Journal of Learning Disabilities, 38(4), 318–323.
Ministry of Education. (2021). The main points of the 2022 revised curriculum review Seoul: Ministry of Education.
Ministry of Education. (2019). 2020 kindergarten curriculum (Ministry of Education Notice No. 2019-189) Seoul: Ministry of Education.
O’Halloran, K. L. (2005). Mathematical discourse: language, symbolism and visual images London, England: Continuum.
Park, S. (2019). The Correlation of musical ability between linguistic ability and mathematical-logic ability. (Master’s thesis). University of Sungshin University, Seoul, Korea.
Paul, R., Norbury, C. F., & Gosse, C. (2017). Language disorders from infancy through adolescence: listening, speaking, reading, writing, and communicating (5th ed .). Mosby: Elsevier, Inc.
Song, K. M. (2010). Correlation of mathematical problem-solving ability to speaking, listening, reading, and writing skills of language arts. (master’s thesis). University of Chuncheon National University of Education, Chuncheon, Korea.
Steffe, L. P. (1992). Learning stages in the construction of the number sequence. In J. Bideaud, C. Meljac, & J. P. Fischer (Eds.), Pathways to number: Children’s developing numerical abilities (pp. 83–98). Hillsdale, NJ: Erlbaum.
Toll, S. W. M., Van der Ven, S. H. G., Kroesbergen, E. H., & Van Luit, J. E. H. (2011). Executive functions as predictors of math learning disabilities. Journal of Learning Disabilities, 44(6), 521–532.
Toll, S. W. M., & Van Luit, J. E. H. (2012). Early numeracy intervention for low-performing kindergartners. Journal of Early Intervention, 34(4), 243–264.
Toll, S. W. M., & Van Luit, J. E. H. (2014). The developmental relationship between language and low early numeracy skills throughout kindergarten. Exceptional Children, 81(1), 64–78.
Whitin, P., & Whitin, D. J. (2000). Math is language too: talking and writing in the mathematics classroom Urbana, Ill: National Council of Teachers of English.
AppendicesAppendix 1.Academic skills: Language and literacy & mathematical thinkingSource: KICCE (Korea Institute of Child Care and Education, https://kicce.re.kr/panel). Appendix 2.Academic performance evaluation questions (Korean, math) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||